已经是最新一篇文章了!
已经是最后一篇文章了!
4. 二维数组中的查找
人学始知道,不学非自然。
4. 二维数组中的查找
题目链接
题目描述
给定一个二维数组,其每一行从左到右递增排序,从上到下也是递增排序。给定一个数,判断这个数是否在该二维数组中。
Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Given target = 5, return true.
Given target = 20, return false.
解题思路
要求时间复杂度 O(M + N),空间复杂度 O(1)。其中 M 为行数,N 为 列数。
该二维数组中的一个数,小于它的数一定在其左边,大于它的数一定在其下边。因此,从右上角开始查找,就可以根据 target 和当前元素的大小关系来快速地缩小查找区间,每次减少一行或者一列的元素。当前元素的查找区间为左下角的所有元素。
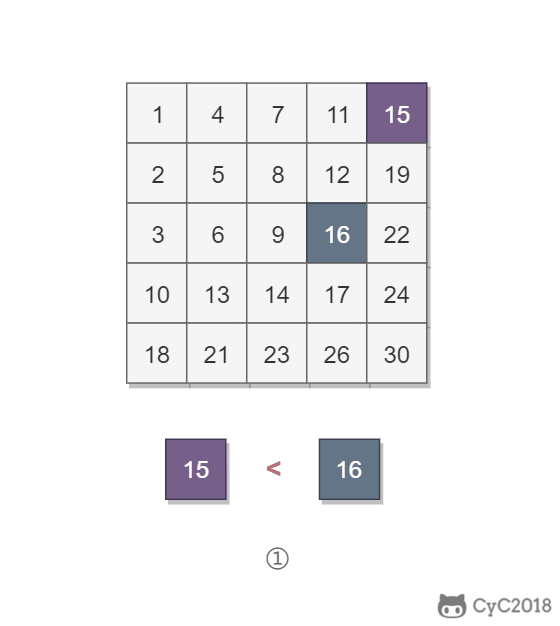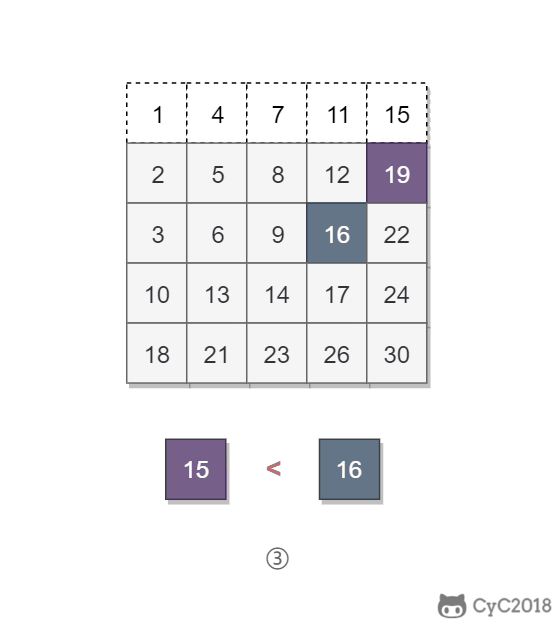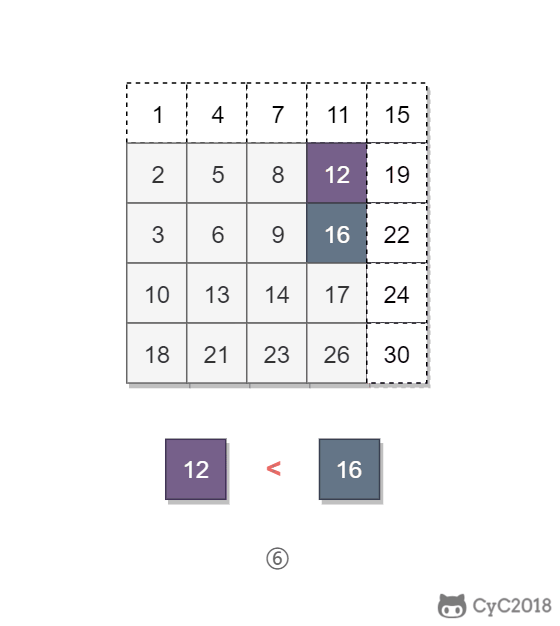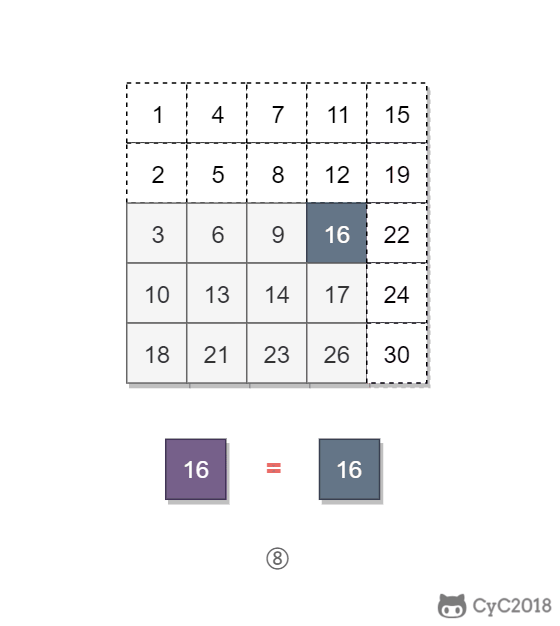
public boolean Find(int target, int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return false;
int rows = matrix.length, cols = matrix[0].length;
int r = 0, c = cols - 1; // 从右上角开始
while (r <= rows - 1 && c >= 0) {
if (target == matrix[r][c])
return true;
else if (target > matrix[r][c])
r++;
else
c--;
}
return false;
}
版权声明:如无特别声明,本站收集的文章归 cs-notes 所有。 如有侵权,请联系删除。
联系邮箱: GenshinTimeStamp@outlook.com
本文标题:《 4. 二维数组中的查找 》

