已经是最新一篇文章了!
已经是最后一篇文章了!
10.4 变态跳台阶
读书不作儒生酸,跃马西入金城关。
10.4 变态跳台阶
题目链接
题目描述
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级… 它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
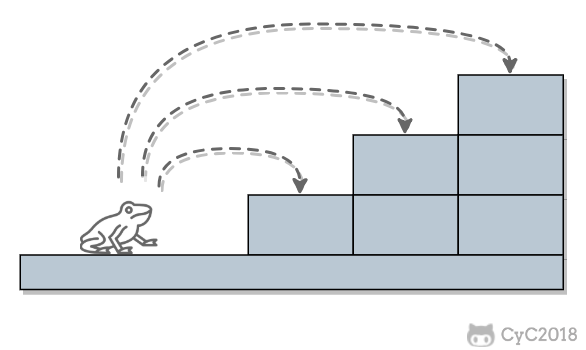
解题思路
动态规划
public int jumpFloorII(int target) {
int[] dp = new int[target];
Arrays.fill(dp, 1);
for (int i = 1; i < target; i++)
for (int j = 0; j < i; j++)
dp[i] += dp[j];
return dp[target - 1];
}
数学推导
跳上 n-1 级台阶,可以从 n-2 级跳 1 级上去,也可以从 n-3 级跳 2 级上去…,那么
f(n-1) = f(n-2) + f(n-3) + ... + f(0)
同样,跳上 n 级台阶,可以从 n-1 级跳 1 级上去,也可以从 n-2 级跳 2 级上去… ,那么
f(n) = f(n-1) + f(n-2) + ... + f(0)
综上可得
f(n) - f(n-1) = f(n-1)
即
f(n) = 2*f(n-1)
所以 f(n) 是一个等比数列
public int JumpFloorII(int target) {
return (int) Math.pow(2, target - 1);
}
版权声明:如无特别声明,本站收集的文章归 cs-notes 所有。 如有侵权,请联系删除。
联系邮箱: GenshinTimeStamp@outlook.com
本文标题:《 10.4 变态跳台阶 》

