已经是最新一篇文章了!
已经是最后一篇文章了!
排序-归并排序
荠花榆荚深村里,亦道春风为我来。
归并排序思想
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。 该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法: * 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法); * 自下而上的迭代;
一、划分
- 当待排序数组 a[ ] 长度 a.length >= 3时,将数组 a [ ] 从 cennter = ( a.length + 1 ) / 2 划分为 left [ 0 ~ center-1 ] , right [ center ~ a.length - 1 ] 。
- 将划分后的数组 left [ ] 和 right [ ] 合并。
- 若数组a [ ] 长度a.length < 3,对该数组直接排序。
- 最后将处理后的数组返回。
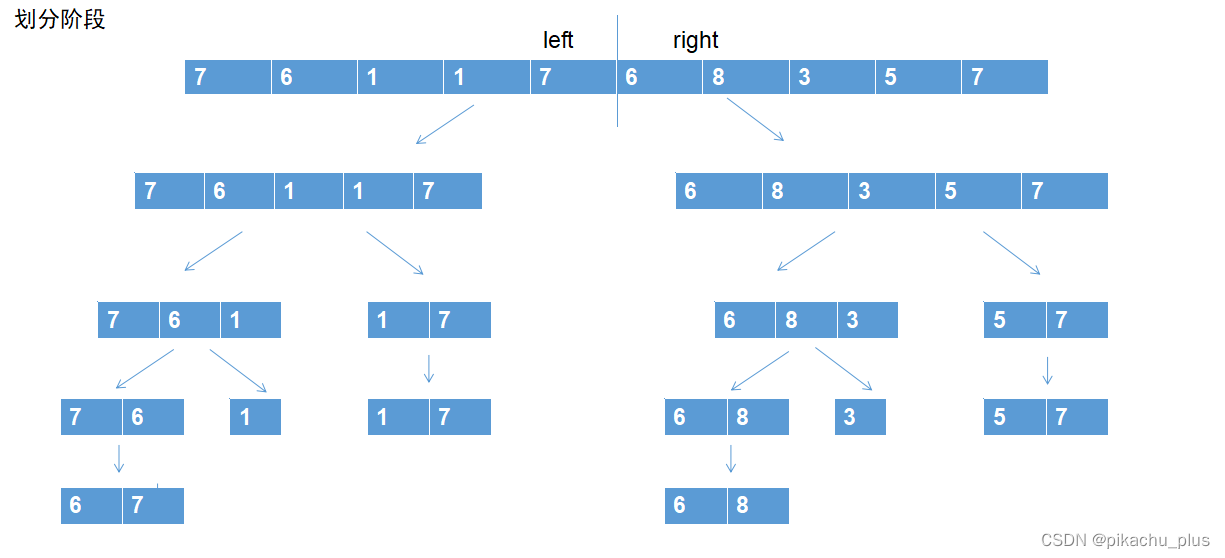 划分阶段——sort()函数进行
划分阶段——sort()函数进行
二、合并
-
初始化合并后的数组为 merge[ ] ,长度为 left.length + right.length 。变量 i ,j,k 初始为0
-
对上一步划分的数组自底向上合并到merge [ ]。
-
i 扫描 left [ ] , j 扫描 right [ ] , k 扫描 merge [ ] 。依次将 left [ i ] 和 right [ j ] 的较小者加入 merge [ k ]。
if (left[i] < right[j]) { merge[k++] = left[i++]; } else { merge[k++] = right[j++]; } -
当 i 或 j 扫描结束时,将剩下的一部分( left [ ] 或 right [ ] 中未全部被扫描的)加入 merge [ ] 。
if (i == left.length) { while (j < right.length) { merge[k++] = right[j++]; } } else if (j == right.length) { while (i < left.length) { merge[k++] = left[i++]; } } 合并阶段———merge()函数进行
合并阶段———merge()函数进行
三、完整代码
import java.util.Arrays;
/**
* @author: pikachu
* @description: 归并排序
* 归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。
* 该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
* 作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
* 自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
* 自下而上的迭代;
* @date: 2022/7/29 21:21
*/
public class Merge {
private static int count = 1;
/**
* Desc:
*
* @param left 待合并数组左半部分
* @param right 待合并数组右半部分
* @return {@link int[]} 合并 left 和 right 后的有序数组
* @author pikachu
*/
private static int[] merge(int[] left, int[] right) {
int[] merge = new int[left.length + right.length];
int i = 0;
int j = 0;
int k = 0;
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
merge[k++] = left[i++];
} else {
merge[k++] = right[j++];
}
}
// 合并剩余部分
if (i == left.length) {
while (j < right.length) {
merge[k++] = right[j++];
}
} else if (j == right.length) {
while (i < left.length) {
merge[k++] = left[i++];
}
}
return merge;
}
public static int[] sort(int[] attr) {
int center = (attr.length + 1) / 2;
if (center > 1) { // 数组长度>=3
// 分
int[] left = Arrays.copyOfRange(attr, 0, center); // 拷贝含头去尾
int[] right = Arrays.copyOfRange(attr, center, attr.length);
left = sort(left);
right = sort(right);
// 治
attr = merge(left, right);
} else if (attr.length == 2 && attr[0] > attr[attr.length - 1]) { // 数组长度 = 2
int temp = attr[0];
attr[0] = attr[attr.length - 1];
attr[attr.length - 1] = temp;
}
return attr;
}
}
class Test16 {
public static void main(String[] args) {
// int[] arr = new int[]{4, 2, 8, 3, 6, 9, 1, 22, 8, 11};
int[] arr = new int[]{7, 6, 1, 1, 7, 6, 8, 3, 5, 7};
// int n = 10;
// int[] arr = new int[n];
// int[] arr1 = new int[n];
// for (int i = 0; i < n; i++) {
// arr[i] = (int) (Math.random() * n);
// arr1[i] = (int) (Math.random() * n);
// }
System.out.println("归并排序前:" + Arrays.toString(arr));
long start = System.currentTimeMillis();
arr = Merge.sort(arr);
long end = System.currentTimeMillis();
System.out.println("归并排序后:" + Arrays.toString(arr));
System.out.println("耗时:" + (end - start) + "毫秒");
// long start1 = System.currentTimeMillis();
// Quick quick = new Quick();
// quick.sort(arr1, 0, arr1.length - 1);
// long end1 = System.currentTimeMillis();
// System.out.println("耗时:" + (end1 - start1) + "毫秒");
// System.out.println("quick.sort()排序后:" + Arrays.toString(arr1));
}
}
四、结果&&速度测试
 结果测试
结果测试
 归并排序与快速排序速度比较
归并排序与快速排序速度比较
版权声明:如无特别声明,本站收集的文章归 HuaJi66/Others 所有。 如有侵权,请联系删除。
联系邮箱: GenshinTimeStamp@outlook.com
本文标题:《 排序-归并排序 》
本文链接:/%E7%AE%97%E6%B3%95/%E6%8E%92%E5%BA%8F/%E6%8E%92%E5%BA%8F_%E5%BD%92%E5%B9%B6%E6%8E%92%E5%BA%8F.html

